Thevenin’s Theorem | DC Network Analysis

 Thevenin’s Theorem

Thevenin’s theorem is the theorem that is applicable where we have to find the voltage or current across any one element in a network without going through the rigorous method of solving a set of network equations.

we usually see in practice that a particular element present in a  circuit is variable and is usually called the load while the other elements present in that circuit are fixed.

Let us consider an example of a household outlet terminal that may be connected to different types of appliances constituting a variable load. Here each time the variable element is changed so the whole circuit has to be analyzed all over again.

To avoid the above-discussed problem, Thevenin’s theorem provides a method by which the fixed part of the circuit is replaced by an equivalent circuit.

Thevenin’s theorem was developed by a french telegraph engineer named M. Leon Thevenin in 1833.

 

Thevenin’s theorem statement

According to Thevenin’s theorem “A linear bilateral network containing one or more independent or dependent voltage or current sources can be replaced by a single voltage source and a series resistor connected to the load”.

The general statement of this theorem is that any linear active network consists of independent and or dependent voltage and current sources and linear bilateral network elements can be replaced by an equivalent circuit consists of a voltage source and a resistance in series.

The voltage source being the open-circuited voltage across the open-circuited load terminal and the resistance is the internal resistance of the source network looking through the open-circuited load terminal.

Steps to solve a network using Thevenin’s theorem

• First of all, remove the load resistance present in the circuit.
• Then find the open-circuit voltage across the open-circuited load terminal(i.e V_OC or V_th).
• Find the equivalent Thevenin’s resistance across the open-circuited terminal(i.e R_th).
• Then obtain Thevenin’s equivalent circuit by connecting a source voltage V_th in series with a series resistance R_th.
• Finally, reconnect the load resistance(R_L ) across the load terminal.

Obviously the load current,

I = V _OC/R_th+R_L.

Different methods to find Thevenin’s equivalent resistance(R_th).

For independent sources: It is the most common method of finding Thevenin’s equivalent resistance. In this method, the voltage source present is to be short-circuited and the current source present is to be open-circuited.

Then the Thevenin’s equivalent resistance R_th for the network is to be calculated by looking through the load terminal kept open-circuited. 

For the circuit containing dependent sources in addition to or in absence of an independent  source:

1stmethod-First of all the voltage across the open-circuited load terminal (V_OC)is calculated by the conventional network analysis. Then short-circuited the load terminal and find the short circuit current(I_SC)through the short-circuited terminal.

i.e  R_th=V_OC/I_SC

2ndmethod–In this method first of all remove the load resistance and applies a dc driving voltage V_dc at the open-circuited load terminal. And all the independent sources are kept deactivated during this time i.e voltage source terminals are shorted and current source terminals are open-circuited.

Then a dc driving due to the application Vdc. Then the value of the Thevenin’s equivalent resistance is given by

R_th =V_dc/I_dc

 

Thevenin’s theorem example

 

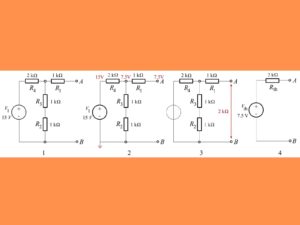
In the above figure, a circuit is given whose V_th, R_th, and Thevenin’s equivalent circuit is to be obtained.

fig.1 shows the original ckt. 

The first step is to find the value of V_th

V_th =(R₂+R₃).V₁/ (R₂+R₃)+R₄

V_th=(1kΩ+1kΩ)×15/(1kΩ+1kΩ)+2kΩ

V_th= 1/2 ×15=7.5

Here it is important to note that R₁ is not considered in the above calculation as it is done in an open circuit condition between A and B so no current will flow through this R1 resistor and therefore will be no voltage drop along this part.

Calculate equivalent Thevenin resistance

R_th =R₁+[(R₂+R₃)||R₄]

=1KΩ+[(1KΩ+1KΩ)||2KΩ]

=1KΩ+( 1 /1KΩ+1K Ω  +  1/2KΩ  )^-1=2KΩ

In this way, we can calculate the value of R_th and V_th for a given circuit.

 

VIEW MORE…