MAXIMUM POWER TRANSFER THEOREM
The Maximum Power Transfer theorem is one of the useful methods in circuit analysis to find the value of load resistance when there would be the maximum transfer of power from the source to load.
Statement of Maximum Power Transfer Theorem
According to this theorem, a resistive load that is being connected in an electrical circuit receives maximum power when the value of the load resistance is equal to the Thevenin’s equivalent resistance for that electrical circuit or load resistance is equal to the internal resistance of the source network as seen from the load terminals.
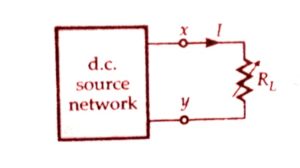
The maximum power transfer theorem is applicable when the load resistance is variable in nature.
Now we will see the complete explanation of this theorem in detail and also we will find the value of maximum power transferred to the load resistance from the source.
Proof of Maximum Power Transfer theorem
Let us consider a variable resistance RL is connected to a dc source network as shown in the figure while another circuit diagram shown below represents the Thevenin voltage VO and the Thevenin resistance RTH of the source network.
Here we will determine the value of RL such that it receives maximum power from the dc source.
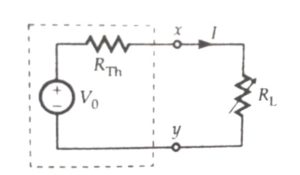
Current ‘I’ in the Thevenin circuit is
I =V0/RTH+RL
Power delivered to the resistive load is
PL =I2 RL
=(V0/RTH+RL )2 .RL
Here, we can see that by varying the load resistance we can maximize the power PL and maximum power that can be delivered to the load can be obtained when dP/dL=0
Then, dP/dL= 1/[RTH+RL]2
[(RTH+RL)2 d/dRL(V02 RL)-V02 RL d/dRL(RTH+RL)]
On solving the above equation and equating the value to zero we get
V02(RTH-RL)/(RTH+RL)3=0
Then,(RTH-RL)=0
Or, RTH=RL
In this way, it has been proved that power transfer to the resistive load from a dc source network is maximum when the value of the load resistance is equal to Thevenin’s equivalent resistance i.e RTH=RL.
By knowing the value of the variable load resistance we can also calculate the value of the maximum power that is transferred to the load resistance.
Pmax = V02 RTH /(RTH+RL)
Pmax = V02/4RTH , (as RL=RTH)
The above value Pmax is the power consumed by the load resistance. And the power transferred by the source is also V02/4RTH.
Then the total power supplied is thus
P=2 V0/4RTH =V02/2RTH
During the maximum power transfer the efficiency
ղ=Pmax/P×100
ղ =V02/4RTH/V02/2RTH * 100
ղ =50%
Steps to solve a network using maximum power transfer theorem
Step 1-First remove the load resistance and find Thevenin equivalent resistance RTh of the source network looking through the open-circuited load terminals.
Step 2- Then this value of RTH is equal to the load resistance for maximum power transfer i.e RTH=RL.
Step 3-find the value of Thevenin’s voltage VTH or V0 across the open-circuited terminals.
Step 4-Then the maximum power transferred to the load is given by Pmax=V02/4RTH.
Application of Maximum Power Transfer Theorem
When we talk about the application of the maximum power transfer theorem it is basically useful in analyzing communication networks because in communication networks the magnitude of power transfer is sufficiently small.
Here the source and load resistances are matched to get maximum power transfer and with the flow of maximum power from the source to the load, low efficiency of 50% is tolerated.
On the other hand in electrical power transmission systems, the value of load resistance is much larger than the source resistance therefore it is difficult to achieve the condition of maximum power transfer ordinarily.
This is the reason due to in power system emphasis is given to keep voltage drops and line losses to a minimum value and hence the operation of the power system, operating with bulk power transmission capability becomes uneconomical if it is operated with 50% efficiency just for the use of maximum power transfer.
Hence in power transmission systems, this criterion of maximum power transfer is rarely used.
