What is a Capacitor? Complete Explanation about Capacitor
Capacitor Definition
A Capacitor is defined as a passive element that is designed to store electrical energy in the form electric field established by the two polarities of charges on the two electrodes of a capacitor. A capacitor consists of two conducting parallel plates which are separated by air, dielectric medium, or an insulator, such as ceramic, waxed paper, mica, and in some cases like in electrolytic capacitor liquid gel are used.

In the capacitor, the presence of a dielectric medium is used to stop the flow of dc current and the blocking of DC current by the insulating material result in voltage build-up across the plates of the capacitor in the form of charge.
Besides resistors, capacitors are the electrical components that are most common in use. Capacitors are one of the most extensively used passive elements in the field of communication, computers, electronics, and power systems.
Capacitance of a Capacitor
The capacitance of a capacitor is the property of a capacitor due to which it can store electric charge in it. In another word, we can also define the capacitance of a capacitor as the capability of an element to store charge within it. Capacitance is also the ratio of charge per unit voltage that is stored in an element. Capacitance is denoted by ‘C’. Farad (F) is the unit of capacitance.
When one coulomb of charge is stored in a capacitor when the voltage across the parallel plates of the capacitor is one volt then the capacitance of the capacitor is ‘1’ farad. Let ‘Q’ be the amount of charge which is stored in a capacitor having capacitance ‘C’ and the potential difference across the plates of the capacitor is ‘V’ volts then capacitance is written as,
C = Q/V
Capacitance ‘C’ of a capacitor also depends on the physical dimensions of the capacitor, then the capacitance of a parallel plate capacitor is given by,
C = εA/D
Here, ε= Permittivity of the dielectric medium (ε=ε0εr)
ε0=Permittivity of free space (ε0=8.854 × 10-12)
εr =relative permittivity
A = Area of each plate of the capacitor
D = distance between a parallel plate of the capacitor
From the above formula of capacitance, we can conclude that the value of capacitance depends on three factors, like the surface area of each plate of the capacitor, the distance between the plates of the capacitor, and the permittivity of the medium present between the plates of the capacitor.
The capacitance of the capacitor is directly proportional to the surface area of the plates, which means the larger the surface area of the plate of the capacitor larger the value of capacitance, Also greater the value of permittivity, greater is the value of capacitance but the value of capacitance is inversely proportional to the distance between the parallel plate of the capacitor, that means smaller the distance between the plates of the capacitor greater will the value of the capacitance.
Symbol of capacitor
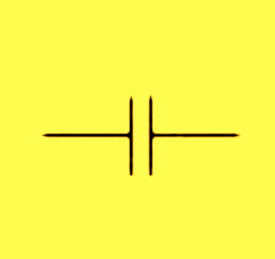
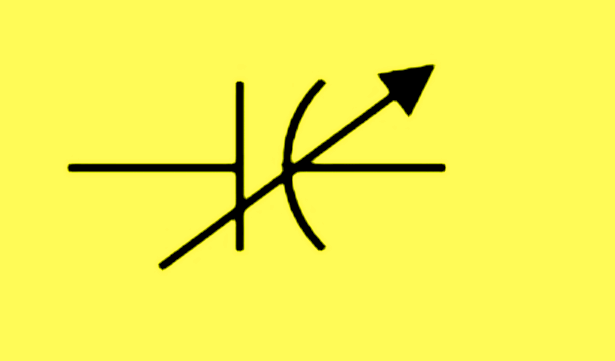
One farad (1 Farad)
Capacitance of a capacitor is ‘1’ farad when a charge of 1 coulomb is accumulated on the plate of the capacitor when ‘1’ volt of the voltage source is applied. 1 farad is numerically written as,
1 farad =1 coulomb/1 volt =9 × 1011 esu
It means ‘1’ farad is equal to 9 × 1011 esu
Here esu= electrostatic unit
A farad is a large unit for the capacitance so, the capacitance of a capacitor is normally represented in microfarad represented as μf, nano farad (nf), and picofarad represented as pf.
Relation between farad and other smaller unit of capacitance is as follow
1 farad = 103mf
1 farad =106μf
1 farad = 109nf
1 farad = 1012pf
Charging process of a capacitor
As we have discussed above a capacitor is a passive element that stores electrical energy in the form of an electrical field. So when a DC voltage source is applied across the capacitor as shown in the figure then a small amount of current will flow due to which charging of capacitor takes place.
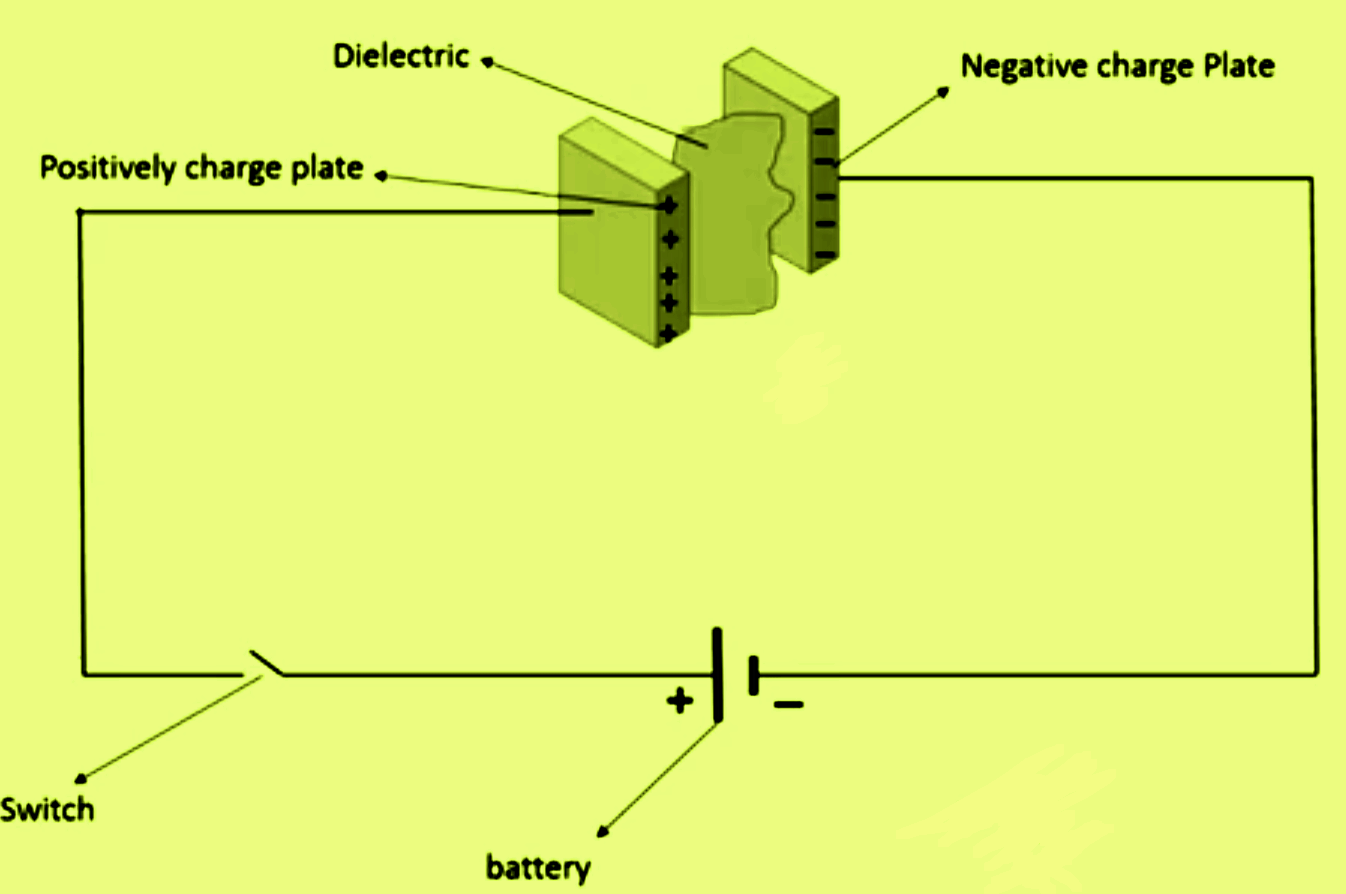
From the above circuit diagram when the switch is turned ON then the negative charges from the negative terminal of the applied DC source move towards plate A of the capacitor and make plate A negatively charge.
On the other side charges from the positive terminal of the applied source voltage moves towards plate B and as a result, plate B is positively charged. By this process, the capacitor is charged by the DC source.
When the switch is turned OFF then the capacitor remains charged for a small interval of time. Due to this stored charge, a current will starts to flow in the capacitor due to the drift of electrons, and this current is called the displacement current.
Charge Stored in a Capacitor
Here we will discuss the charge stored in a capacitor. Let us consider a voltage source having voltage ‘V’ is applied across the parallel plate capacitor as shown in the figure.
Due to the applied voltage V, a positive charge q is deposited on one of the plates of the capacitor, and on the other plate a negative charge’-q ’is also deposited by the applied source voltage as shown in the figure.
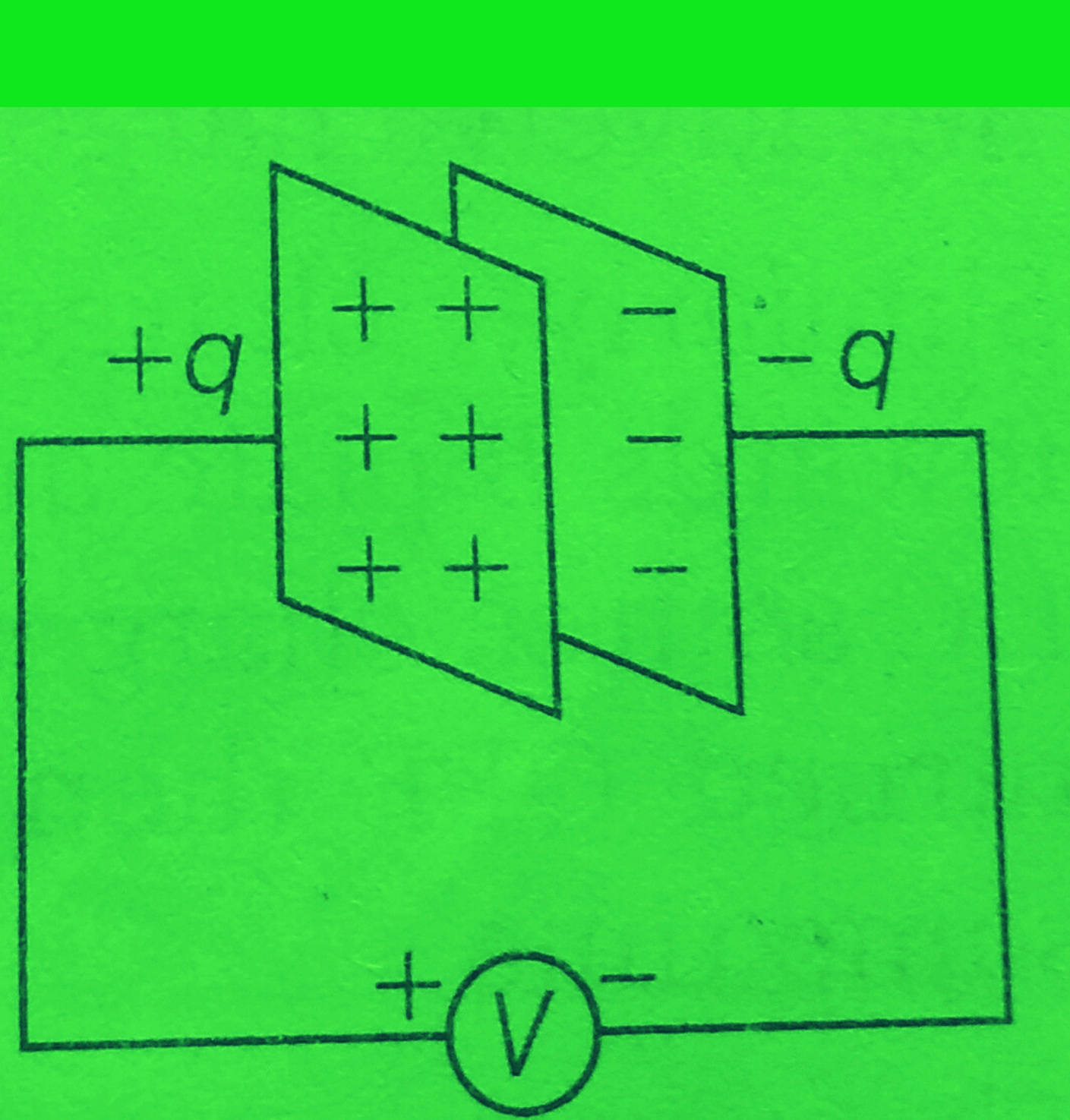
Here it is said that capacitor stores an electric charge. The amount of electric charge stored in the capacitor is represented by ‘q’ and this stored charge is directly proportional to the applied source voltage ‘V’.
Let q = charged stored in the capacitor, in coulomb
V= applied source voltage, in volt
C= capacitance of the capacitor in farad
q directly proportional V
q/v = constant
q/v = C
q = CV
Stored charge in the capacitor, q = CV
Energy stored in a capacitor
As we know that DC current does not flow continuously due to the presence of insulating material or dielectric present between the plates of the capacitor so instead of this DC current electrical energy is stored in the form of an electric field.
We know the value of C =q/v
i= C dv/dt (since, i= dq/dt)
dv = 1/c ×i ×dt
v = 1/c ∫ i.dt (volt)
We know that, power P = V.i
P = V×C ×dv/dt
P = C ×V×dv/dt = instantaneous power
Instantaneous energy ‘E’ =∫P.dt (joule) ………… equation (1)
E =∫C.V (dv/dt )
As P = C ×V × dv/dt
P =d/dt ( ½C v2 )……… equation (2)
From equation (1) and equation (2) we get,
E= ½ CV2
Therefore the energy stored inside a capacitor is equal to ½ CV2.
AS we have seen above that capacitor store electrical energy, and a battery also store electrical energy but a capacitor is different from a battery in every aspect which is given below.½ CV2.
Difference between Battery and Capacitor
| Battery | Capacitor |
| Batteries have chemicals inside. | Capacitors have electrical plates inside. |
| The charge is stored for a longer time in a battery. | The charge is stored for a shorter time in a capacitor. |
| The charge is stored in the chemicals. | The charge is stored in the plates. |
| It is used to provide long-time energy in a circuit. | It is used to provide short-time energy in a circuit. |
I hope you like this article on ‘what is a Capacitor”. Any Suggestions, Please Comment Below.
